In this post, we will learn about Eigenface — an application of Principal Component Analysis (PCA) for human faces. We will also share C++ and Python code written using OpenCV to explain the concept.
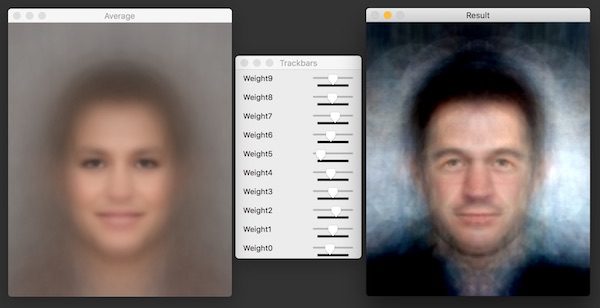
The video below shows a demo of EigenFaces. The code for the application shown in the video is shared in this post.
What is PCA?
In our previous post, we learned about a dimensionality reduction technique called PCA. If you have not read the post, please do so. It is a pre-requisite for understanding this post.
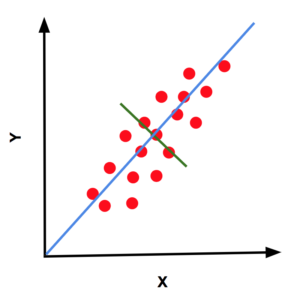
To quickly recap, we learned that the first principal component is the direction of maximum variance in the data. The second principal component is the direction of maximum variance in the space perpendicular (orthogonal) to the first principal component and so on and so forth. The first and second principal components the red dots (2D data) are shown using blue and green lines.
We also learned that the first principal component is the eigenvector of the covariance matrix corresponding to the maximum eigenvalue. The second principal component is the eigenvector corresponding to the second largest eigenvalue. If what was said in this paragraph is not clear to you, it is a good idea to brush up your understanding of PCA by reading the previous post
What are EigenFaces ?
Eigenfaces are images that can be added to a mean (average) face to create new facial images. We can write this mathematically as,
![\[F = F_m + \sum^n_{i=1} \alpha_i F_i\]](https://learnopencv.com/wp-content/ql-cache/quicklatex.com-b60d8db7af6c0d15bc997c6bf060383a_l3.png)
where,
![]() is a new face.
is a new face.![]() is the mean or the average face,
is the mean or the average face,![]() is an EigenFace,
is an EigenFace,![]() are scalar multipliers we can choose to create new faces. They can be positive or negative.
are scalar multipliers we can choose to create new faces. They can be positive or negative.
Eigenfaces are calculated by estimating the principal components of the dataset of facial images. They are used for applications like Face Recognition and Facial Landmark Detection.
An Image as a Vector
In the previous post, all examples shown were 2D or 3D data points. We learned that if we had a collection of these points, we can find the principal components. But how do we represent an image as a point in a higher dimensional space? Let’s look at an example.
A 100 x 100 color image is nothing but an array of 100 x 100 x 3 ( one for each R, G, B color channel ) numbers. Usually, we like to think of 100 x 100 x 3 array as a 3D array, but you can think of it as a long 1D array consisting of 30,000 elements.
You can think of this array of 30k elements as a point in a 30k-dimensional space just as you can imagine an array of 3 numbers (x, y, z) as a point in a 3D space!
How do you visualize a 30k dimensional space? You can’t. Most of the time you can build your argument as if there were only three dimensions, and usually ( but not always ), they hold true for higher dimensional spaces as well.
How to calculate EigenFaces?
To calculate EigenFaces, we need to use the following steps.
- Obtain a facial image dataset : We need a collection of facial images containing different kinds of faces. In this post, we used about 200 images from CelebA.
- Align and resize images : Next we need to align and resize images so the center of the eyes are aligned in all images. This can be done by first finding facial landmarks. In this post, we used aligned images supplied in CelebA. At this point, all the images in the dataset should be the same size.
- Create a data matrix: Create a data matrix containing all images as a row vector. If all the images in the dataset are of size 100 x 100 and there are 1000 images, we will have a data matrix of size 30k x 1000.
- Calculate Mean Vector [Optional]: Before performing PCA on the data, we need to subtract the mean vector. In our case, the mean vector will be a 30k x 1 row vector calculated by averaging all the rows of the data matrix. The reason calculating this mean vector is not necessary for using OpenCV’s PCA class is because OpenCV conveniently calculates the mean for us if the vector is not supplied. This may not be the case in other linear algebra packages.
- Calculate Principal Components: The principal components of this data matrix are calculated by finding the Eigenvectors of the covariance matrix. Fortunately, the PCA class in OpenCV handles this calculation for us. We just need to supply the datamatrix, and out comes a matrix containing the Eigenvectors
- Reshape Eigenvectors to obtain EigenFaces: The Eigenvectors so obtained will have a length of 30k if our dataset contained images of size 100 x 100 x 3. We can reshape these Eigenvectors into 100 x 100 x 3 images to obtain EigenFaces.
Principal Component Analysis (PCA) using OpenCV
The PCA class in OpenCV allows us to compute the principal components of a data matrix. Read the documentation for different usages. Here we are discussing the most common way to use the PCA class.
C++
// Example usage
PCA pca(data, Mat(), PCA::DATA_ORDER_ROW, 10);
Mat mean = pca.mean;
Mat eigenVectors = pca.eigenvectors;
Python
// Example usage
mean, eigenVectors = cv2.PCACompute(data, mean=None, maxComponents=10)
where,
| data | The data matrix containing every data point as either a row or a column vector. If our data consists of 1000 images, and each image is a 30k long row vector, the data matrix will of size 30k x 1000. |
| mean | The average of the data. If every data point in the data matrix is a 30k long row vector, the mean will also be a vector of the same size. This parameter is optional and is calculated internally if it is not supplied. |
| flags | It can take values DATA_AS_ROW or DATA_AS_COL indicating whether a point in the data matrix is arranged along the row or along the column. In the code we have shared, we have arranged it as a row vector. Note : In the Python version, you do not have the option of specifying this flag. The data needs to have one image in one row. |
| maxComponents | The maximum number of principal components is usually the smaller of the two values 1) Dimensionality of the original data ( in our case it is 30k ) 2) The number of data points ( e.g. 1000 in the above example ). However, we can explicity fix the maximum number of components we want to calculate by setting this argument. For example, we may be interested in only the first 50 principal components. Calculating fewer principal components is cheaper than calculating the theoretical max. |
EigenFace : C++ and Python Code
In this section, we will examine the relevant parts of the code. The credit for the code goes to Subham Rajgaria . He wrote this code as part of his internship at our company Big Vision LLC.
Let’s go over the main function in both C++ and Python. Look for the explanation and expansion of the functions used after this code block.
C++
#define NUM_EIGEN_FACES 10
#define MAX_SLIDER_VALUE 255
int main(int argc, char **argv)
{
// Directory containing images
string dirName = "images/";
// Read images in the directory
vector<Mat> images;
readImages(dirName, images);
// Size of images. All images should be the same size.
Size sz = images[0].size();
// Create data matrix for PCA.
Mat data = createDataMatrix(images);
// Calculate PCA of the data matrix
cout << "Calculating PCA ...";
PCA pca(data, Mat(), PCA::DATA_AS_ROW, NUM_EIGEN_FACES);
cout << " DONE"<< endl;
// Extract mean vector and reshape it to obtain average face
averageFace = pca.mean.reshape(3,sz.height);
// Find eigen vectors.
Mat eigenVectors = pca.eigenvectors;
// Reshape Eigenvectors to obtain EigenFaces
for(int i = 0; i < NUM_EIGEN_FACES; i++)
{
Mat eigenFace = eigenVectors.row(i).reshape(3,sz.height);
eigenFaces.push_back(eigenFace);
}
// Show mean face image at 2x the original size
Mat output;
resize(averageFace, output, Size(), 2, 2);
namedWindow("Result", CV_WINDOW_AUTOSIZE);
imshow("Result", output);
// Create trackbars
namedWindow("Trackbars", CV_WINDOW_AUTOSIZE);
for(int i = 0; i < NUM_EIGEN_FACES; i++)
{
sliderValues[i] = MAX_SLIDER_VALUE/2;
createTrackbar( "Weight" + to_string(i), "Trackbars", &sliderValues[i], MAX_SLIDER_VALUE, createNewFace);
}
// You can reset the sliders by clicking on the mean image.
setMouseCallback("Result", resetSliderValues);
cout << "Usage:" << endl
<< "\tChange the weights using the sliders" << endl
<< "\tClick on the result window to reset sliders" << endl
<< "\tHit ESC to terminate program." << endl;
waitKey(0);
destroyAllWindows();
}
Python
if __name__ == '__main__':
# Number of EigenFaces
NUM_EIGEN_FACES = 10
# Maximum weight
MAX_SLIDER_VALUE = 255
# Directory containing images
dirName = "images"
# Read images
images = readImages(dirName)
# Size of images
sz = images[0].shape
# Create data matrix for PCA.
data = createDataMatrix(images)
# Compute the eigenvectors from the stack of images created
print("Calculating PCA ", end="...")
mean, eigenVectors = cv2.PCACompute(data, mean=None, maxComponents=NUM_EIGEN_FACES)
print ("DONE")
averageFace = mean.reshape(sz)
eigenFaces = [];
for eigenVector in eigenVectors:
eigenFace = eigenVector.reshape(sz)
eigenFaces.append(eigenFace)
# Create window for displaying Mean Face
cv2.namedWindow("Result", cv2.WINDOW_AUTOSIZE)
# Display result at 2x size
output = cv2.resize(averageFace, (0,0), fx=2, fy=2)
cv2.imshow("Result", output)
# Create Window for trackbars
cv2.namedWindow("Trackbars", cv2.WINDOW_AUTOSIZE)
sliderValues = []
# Create Trackbars
for i in xrange(0, NUM_EIGEN_FACES):
sliderValues.append(MAX_SLIDER_VALUE/2)
cv2.createTrackbar( "Weight" + str(i), "Trackbars", MAX_SLIDER_VALUE/2, MAX_SLIDER_VALUE, createNewFace)
# You can reset the sliders by clicking on the mean image.
cv2.setMouseCallback("Result", resetSliderValues);
print('''Usage:
Change the weights using the sliders
Click on the result window to reset sliders
Hit ESC to terminate program.''')
cv2.waitKey(0)
cv2.destroyAllWindows()
The above code does the following.
- Set the number of Eigenfaces (NUM_EIGEN_FACES) to 10 and the max value of the sliders (MAX_SLIDER_VALUE) to 255. These numbers are not set in stone. Change these numbers to see how the application changes.
- Read Images : Next we read all images in the specified directory using the function readImages. The directory contains images that are aligned. The center of the left and the right eyes in all images are the same. We add these images to a list ( or vector ). We also flip the images vertically and add them to the list. Because the mirror image of a valid facial image, we just doubled the size of our dataset and made it symmetric at that same time.
- Assemble Data Matrix: Next, we use the function createDataMatrix to assemble the images into a data matrix. Each row of the data matrix is one image. Let’s look into the createDataMatrix function
C++
// Create data matrix from a vector of images
static Mat createDataMatrix(const vector<Mat> &images)
{
cout << "Creating data matrix from images ...";
// Allocate space for all images in one data matrix.
// The size of the data matrix is
//
// ( w * h * 3, numImages )
//
// where,
//
// w = width of an image in the dataset.
// h = height of an image in the dataset.
// 3 is for the 3 color channels.
Mat data(static_cast<int>(images.size()), images[0].rows * images[0].cols * 3, CV_32F);
// Turn an image into one row vector in the data matrix
for(unsigned int i = 0; i < images.size(); i++)
{
// Extract image as one long vector of size w x h x 3
Mat image = images[i].reshape(1,1);
// Copy the long vector into one row of the destm
image.copyTo(data.row(i));
}
cout << " DONE" << endl;
return data;
}
Python
def createDataMatrix(images):
print("Creating data matrix",end=" ... ")
'''
Allocate space for all images in one data matrix.
The size of the data matrix is
( w * h * 3, numImages )
where,
w = width of an image in the dataset.
h = height of an image in the dataset.
3 is for the 3 color channels.
'''
numImages = len(images)
sz = images[0].shape
data = np.zeros((numImages, sz[0] * sz[1] * sz[2]), dtype=np.float32)
for i in range(0, numImages):
image = images[i].flatten()
data[i,:] = image
print("DONE")
return data
4. Calculate PCA : Next we calculate the PCA using the PCA class in C++ (see lines 19-23 in the main function above) and the PCACompute function in Python (see line 23 in the main function above). As an output of PCA, we obtain the mean vector and the 10 Eigenvectors.
5. Reshape vectors to obtain Average Face and EigenFaces : The mean vector and every Eigenvector is vector of length w * h * 3, where w is the width, h is the height and 3 is the number of color channels of any image in the dataset. In other words, they are vectors of 30k elements. We reshape them to the original size of the image to obtain the average face and the EigenFaces. See line 24-35 in the C++ code and lines 26-32 in Python code.
6. Create new face based on slider values. A new face can be created by adding weighted EigenFaces to the average face using the function createNewFace. In OpenCV, slider values cannot be negative. So we calculate the weights by subtracting MAX_SLIDER_VALUE/2 from the current slider value so we can get both positive and negative values.
C++
void createNewFace(int ,void *)
{
// Start with the mean image
Mat output = averageFace.clone();
// Add the eigen faces with the weights
for(int i = 0; i < NUM_EIGEN_FACES; i++)
{
// OpenCV does not allow slider values to be negative.
// So we use weight = sliderValue - MAX_SLIDER_VALUE / 2
double weight = sliderValues[i] - MAX_SLIDER_VALUE/2;
output = output + eigenFaces[i] * weight;
}
resize(output, output, Size(), 2, 2);
imshow("Result", output);
}
Python
def createNewFace(*args):
# Start with the mean image
output = averageFace
# Add the eigen faces with the weights
for i in range(0, NUM_EIGEN_FACES):
'''
OpenCV does not allow slider values to be negative.
So we use weight = sliderValue - MAX_SLIDER_VALUE / 2
'''
sliderValues[i] = cv2.getTrackbarPos("Weight" + str(i), "Trackbars");
weight = sliderValues[i] - MAX_SLIDER_VALUE/2
output = np.add(output, eigenFaces[i] * weight)
# Display Result at 2x size
output = cv2.resize(output, (0,0), fx=2, fy=2)
cv2.imshow("Result", output)