In this post, we will learn how to find the Convex Hull of a shape (a group of points). We will briefly explain the algorithm and then follow up with C++ and Python code implementation using OpenCV.
What is a Convex Hull?
Let us break the term down into its two parts — Convex and Hull.
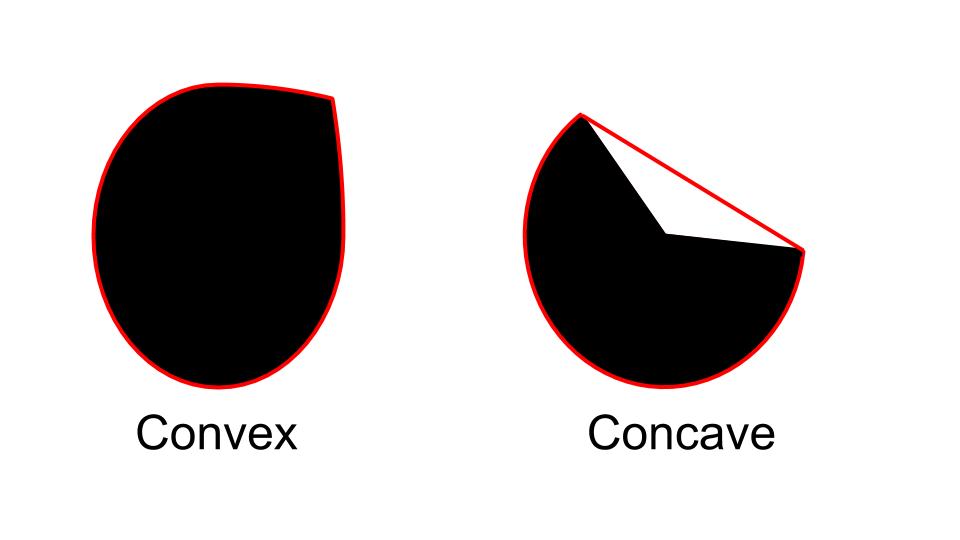
A Convex object is one with no interior angles greater than 180 degrees. A shape that is not convex is called Non-Convex or Concave. An example of a convex and a non-convex shape is shown in Figure 1.
Hull means the exterior or the shape of the object.
Therefore, the Convex Hull of a shape or a group of points is a tight fitting convex boundary around the points or the shape.
The Convex Hull of the two shapes in Figure 1 is shown in Figure 2. The Convex Hull of a convex object is simply its boundary. The Convex Hull of a concave shape is a convex boundary that most tightly encloses it.
Gift Wrapping Algorithms
Given a set of points that define a shape, how do we find its convex hull? The algorithms for finding the Convext Hull are often called Gift Wrapping algorithms. The video below explains a few algorithms with excellent animations:
Easy, huh? A lot of things look easy on the surface, but as soon as we impose certain constraints on them, things become pretty hard.
For example, the Jarvis March algorithm described in the video has complexity O(nh) where n is the number of input points and h is the number of points in the convex hull. Chan’s algorithm has complexity O(n log h).
Is an O(n) algorithm possible? The answer is YES, but boy the history of finding a linear algorithm for convex hull is a tad embrassing.
The first O(n) algorithm was published by Sklansky in 1972. It was later proven to be incorrect. Between 1972 and 1989, 16 different linear algorithms were published and 7 of them were found to be incorrect later on!
This reminds me of a joke I heard in college. Every difficult problem in mathematics has a simple, easy to understand wrong solution!
Now, here is an embarrassing icing on the embarrassing cake. The algorithm implemented in OpenCV is one by Sklansky (1982). It happens to be INCORRECT!
It is still a popular algorithm and in a vast majority of cases, it produces the right result. This algorithm is implemented in the convexHull class in OpenCV. Let’s now see how to use it.
convexHull in OpenCV
By now we know the Gift Wrapping algorithms for finding the Convex Hull work on a collection of points.
How do we use it on images?
We first need to binarize the image we are working with, find contours and finally find the convex hull. Let’s go step by step.
Step 1: Read the Input Image
Python
src = cv2.imread("sample.jpg", 1) # read input image
C++
Mat src;
src = imread("sample.jpg", 1); // read input image
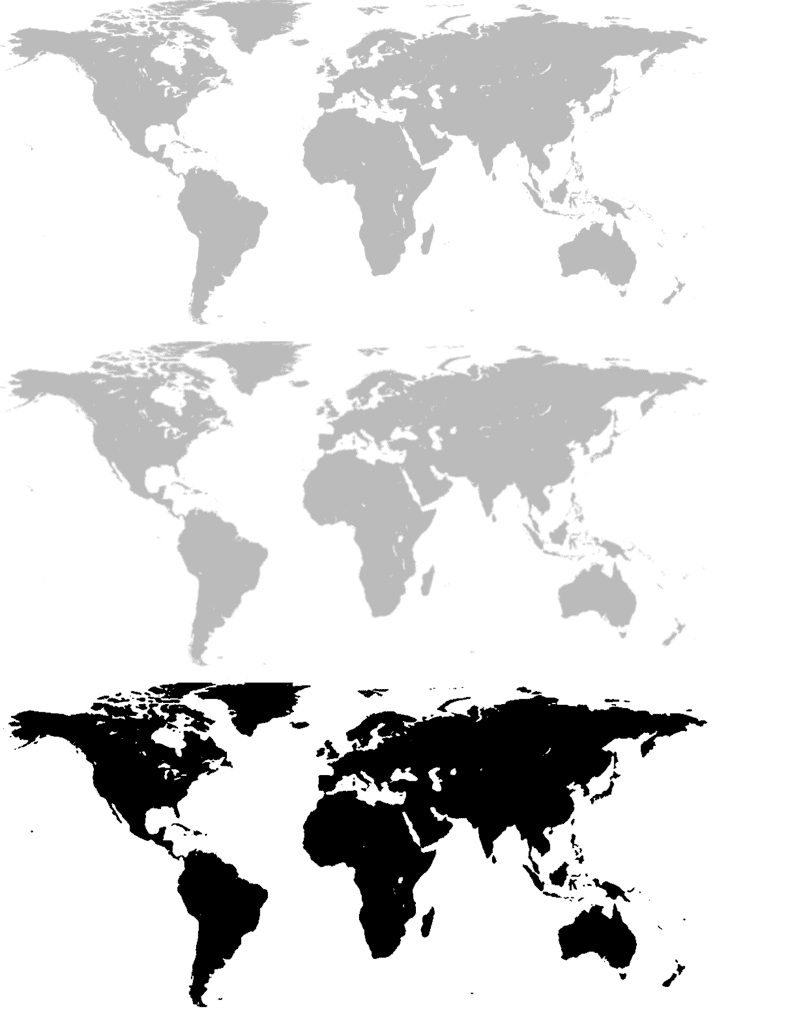
Step 2: Binarize the input image
We perform binarization in three steps —
- Convert to grayscale
- Blur to remove noise
- Threshold to binarize image
The results of these steps are shown in Figure 3. And here is the code.
Python
gray = cv2.cvtColor(src, cv2.COLOR_BGR2GRAY) # convert to grayscale
blur = cv2.blur(gray, (3, 3)) # blur the image
ret, thresh = cv2.threshold(blur, 50, 255, cv2.THRESH_BINARY)
C++
Mat gray, blur_image, threshold_output;
cvtColor(src, gray, COLOR_BGR2GRAY); // convert to grayscale
blur(gray, blur_image, Size(3, 3)); // apply blur to grayscaled image
threshold(blur_image, threshold_output, 50, 255, THRESH_BINARY); // apply binary thresholding
As you can see, we have converted the image into binary blobs. We next need to find the boundaries of these blobs.
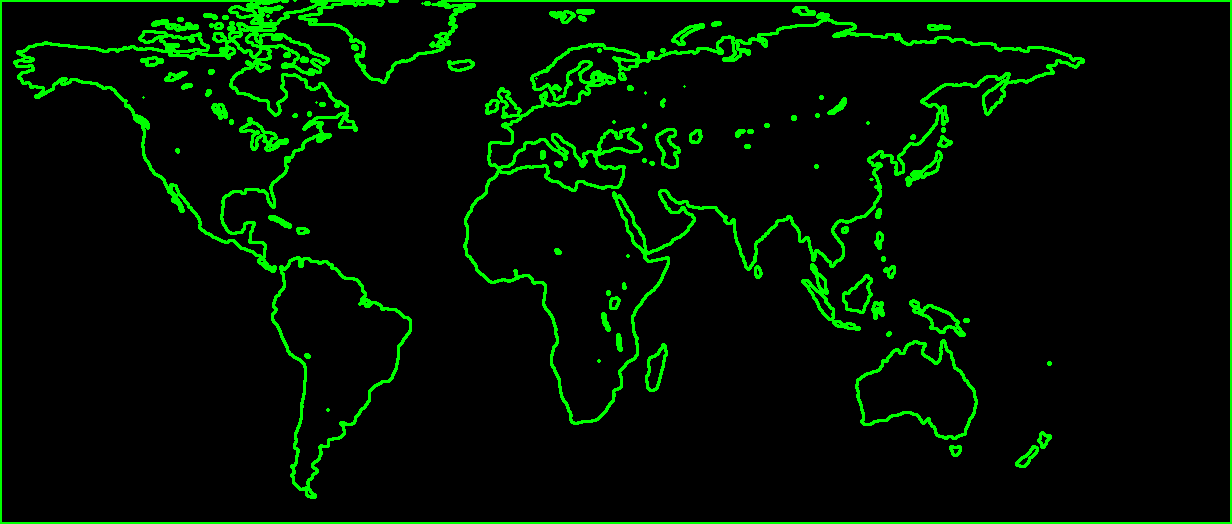
Step 3: Use findContour to find contours
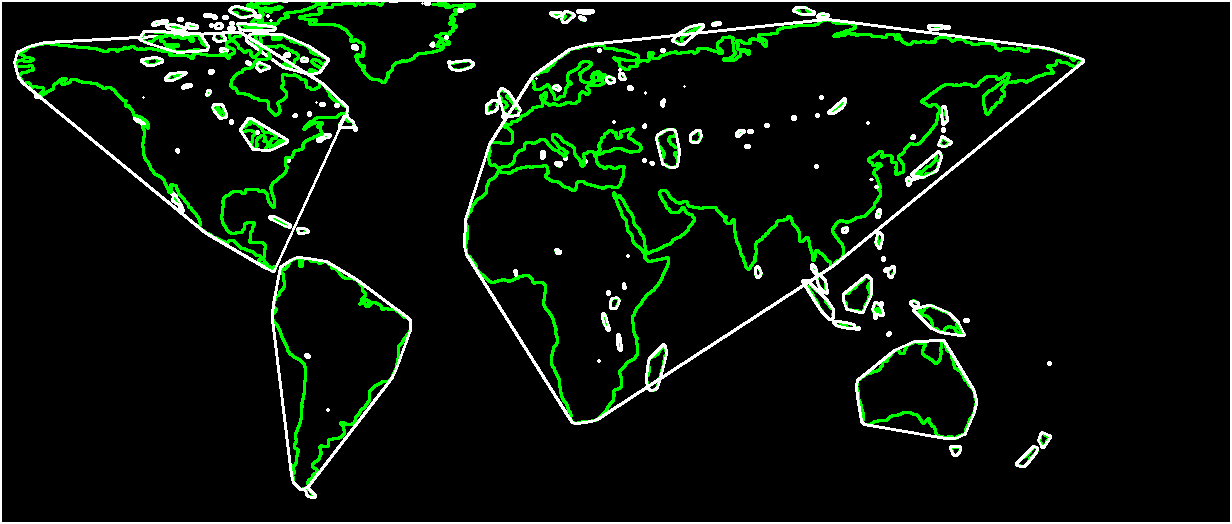
Next, we find the contour around every continent using the findContour function in OpenCV. Finding the contours gives us a list of boundary points around each blob.
If you are a beginner, you may be tempted to think why we did not simply use edge detection? Edge detection would have simply given us locations of the edges. But we are interested in finding how edges are connected to each other. findContour allows us to find those connections and returns the points that form a contour as a list.
Python
# Finding contours for the thresholded image
im2, contours, hierarchy = cv2.findContours(thresh, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)
C++
vector< vector<Point> > contours; // list of contour points
vector<Vec4i> hierarchy;
// find contours
findContours(threshold_output, contours, hierarchy, RETR_TREE, CHAIN_APPROX_SIMPLE, Point(0, 0));
Step 4: Find the Convex Hull using convexHull
Since we have found the contours, we can now find the Convex Hull for each of the contours. This can be done using convexHull function.
Python
# create hull array for convex hull points
hull = []
# calculate points for each contour
for i in range(len(contours)):
# creating convex hull object for each contour
hull.append(cv2.convexHull(contours[i], False))
C++
// create hull array for convex hull points
vector< vector<Point> > hull(contours.size());
for(int i = 0; i < contours.size(); i++)
convexHull(Mat(contours[i]), hull[i], False);
Step 5: Draw the Convex Hull
The final step is to visualize the convex hulls we have just found. Of course a convex hull itself is just a contour and therefore we can use OpenCV’s drawContours.
Python
# create an empty black image
drawing = np.zeros((thresh.shape[0], thresh.shape[1], 3), np.uint8)
# draw contours and hull points
for i in range(len(contours)):
color_contours = (0, 255, 0) # green - color for contours
color = (255, 0, 0) # blue - color for convex hull
# draw ith contour
cv2.drawContours(drawing, contours, i, color_contours, 1, 8, hierarchy)
# draw ith convex hull object
cv2.drawContours(drawing, hull, i, color, 1, 8)
C++
// create a blank image (black image)
Mat drawing = Mat::zeros(threshold_output.size(), CV_8UC3);
for(int i = 0; i < contours.size(); i++) [
Scalar color_contours = Scalar(0, 255, 0); // green - color for contours
Scalar color = Scalar(255, 0, 0); // blue - color for convex hull
// draw ith contour
drawContours(drawing, contours, i, color_contours, 1, 8, vector<Vec4i>(), 0, Point());
// draw ith convex hull
drawContours(drawing, hull, i, color, 1, 8, vector<Vec4i>(), 0, Point());
}
Applications of Convex Hull
There are several applications of the convex hull. Let’s explore a couple of them.
Boundary from a set of points
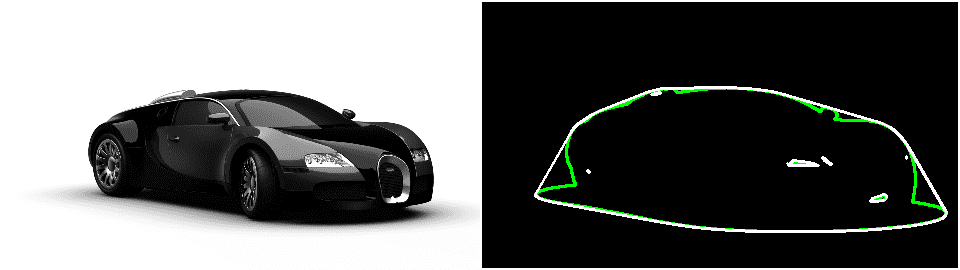
Regular readers of this blog may be aware we have used convexHull before in our face swap application. Given the facial landmarks detected using Dlib, we found the boundary of the face using the convex hull as shown in Figure 6.
There are several other applications, where we recover feature points information instead of contour information. For example, in many active lighting systems like Kinect, we recover a grayscale depth map that is a collection of points. We can use the convex hull of these points to locate the boundary of an object in the scene.
Collision Avoidance
Imagine a car as a set of points and the polygon (minimal set) containing all the points. Now if the convex hull is able to avoid the obstacles, so should the car. Finding the intersection between arbitrary contours is computationally much more expensive than finding the collision between two convex polygons. So you are better off using a convex hull for collision detection or avoidance.