fbpx

LearnOpenCV

Image Alignment (ECC) in OpenCV ( C++ / Python )

Satya Mallick
July 1, 2015 69 Comments
Computer Vision Stories Image Alignment OpenCV 3

By 69 Comments

Image Alignment Example OpenCV
Figure 1. Left: An image from the Prokudin-Gorskii Collection. Right : The same image with the channels aligned.

The image on the left is part of a historic collection of photographs called the Prokudin-Gorskii collection. The image was taken by a Russian photographer in the early 1900s using one of the early color cameras. The color channels of the image are misaligned because of the mechanical nature of the camera. The image on the right is a version of the same image with the channels brought into alignment using a function available in OpenCV 3.

You can download the code for all the examples shown in this post from the download section located at the bottom of the post.

In this post we will embark on a fun and entertaining journey into the history of color photography while learning about image alignment in the process. This post is dedicated to the early pioneers of color photography who have enabled us to capture and store our memories in color.

A Brief and Incomplete History of Color Photography

Ribbon by Maxell and Sutton was the first color photo
Figure 2. Ribbon by Maxwell and Sutton was the first color photo ever taken by superimposing 3 grayscale images.

The idea that you can take three different photos using three primary color filters (Red, Green, Blue) and combine them to obtain a color image was first proposed by James Clerk Maxwell ( yes, the Maxwell ) in 1855. Six years later, in 1861, English photographer Thomas Sutton produced the first color photograph by putting Maxwell’s theory into practice. He took three grayscale images of a Ribbon ( see Figure 2 ), using three different color filters and then superimposed the images using three projectors equipped with the same color filters. The photographic material available at that time was sensitive to blue light, but not very sensitive to green light, and almost insensitive to red light. Although revolutionary for its time, the method was not practical.

By the early 1900s, the sensitivity of photographic material had improved substantially, and in the first decade of the century a few different practical cameras were available for color photography. Perhaps the most popular among these cameras, the Autochrome, was invented by the Lumière brothers.

A competing camera system was designed by Adolf Miethe and built by Wilhelm Bermpohl, and was called Professor Dr. Miethe’s Dreifarben-Camera. In German the word “Dreifarben” means tri-color. This camera, also referred to as the Miethe-Bermpohl camera, had a long glass plate on which the three images were acquired with three different filters. A very good description and an image of the camera can be found here.

Master Generative AI for CV

Get expert guidance, insider tips & tricks. Create stunning images, learn to fine tune diffusion models, advanced Image editing techniques like In-Painting, Instruct Pix2Pix and many more
Three images captured on a vertical glass plate by Miethe-Bermpohl camera .
Figure 3 : Three images captured on a vertical glass plate by a Miethe-Bermpohl camera .

In the hands of Sergey Prokudin-Gorskii the Miethe-Bermpohl camera ( or a variant of it ) would secure a special place in Russian history . In 1909, with funding from Tsar Nicholas II, Prokudin-Gorskii started a decade long journey of capturing Russia in color! He took more than 10,000 color photographs. The most notable among his photographs is the only known color photo of Leo Tolstoy.

Fortunately for us, the Library of Congress purchased a large collection of Prokudin-Gorskii’s photographs in 1948. They are now in the public domain and we get a chance to reconstruct Russian history in color!

It is not trivial to generate a color image from these black and white images (shown in Figure 3). The Miethe-Bermpohl camera was a mechanical device that took these three images over a span of 2-6 seconds. Therefore the three channels were often mis-aligned, and naively stacking them up leads to a pretty unsatisfactory result shown in Figure 1.

Well, it’s time for some vision magic!

Motion models in OpenCV

In a typical image alignment problem we have two images of a scene, and they are related by a motion model. Different image alignment algorithms aim to estimate the parameters of these motion models using different tricks and assumptions. Once these parameters are known, warping one image so that it aligns with the other is straight forward.

Let’s quickly see what these motion models look like.

OpenCV Motion Models
Figure 4. This shows how the image of a square gets transformed by different motion models.

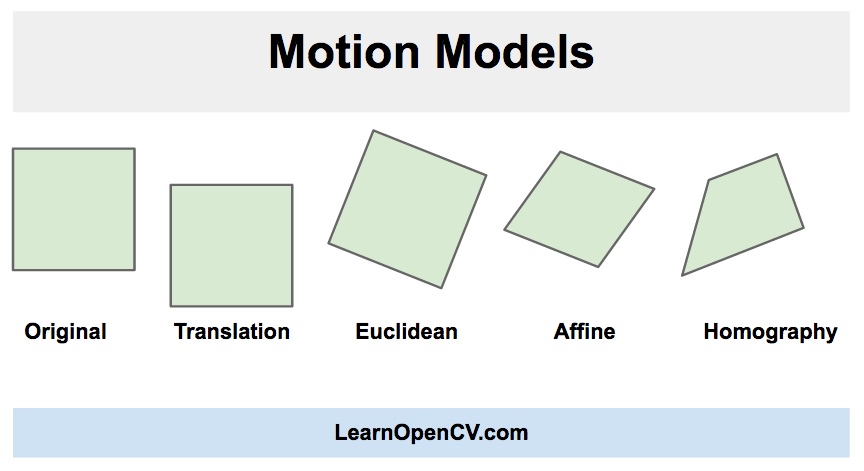
The OpenCV constants that represent these models have a prefix MOTION_ and are shown inside the brackets.

  1. Translation ( MOTION_TRANSLATION ) : The first image can be shifted ( translated ) by (x , y) to obtain the second image. There are only two parameters x and y that we need to estimate.
  2. Euclidean ( MOTION_EUCLIDEAN ) : The first image is a rotated and shifted version of the second image. So there are three parameters — x, y and angle . You will notice in Figure 4, when a square undergoes Euclidean transformation, the size does not change, parallel lines remain parallel, and right angles remain unchanged after transformation.
  3. Affine ( MOTION_AFFINE ) : An affine transform is a combination of rotation, translation ( shift ), scale, and shear. This transform has six parameters. When a square undergoes an Affine transformation, parallel lines remain parallel, but lines meeting at right angles no longer remain orthogonal.
  4. Homography ( MOTION_HOMOGRAPHY ) : All the transforms described above are 2D transforms. They do not account for 3D effects. A homography transform on the other hand can account for some 3D effects ( but not all ). This transform has 8 parameters. A square when transformed using a Homography can change to any quadrilateral.

In OpenCV an Affine transform is stored in a 2 x 3 sized matrix. Translation and Euclidean transforms are special cases of the Affine transform. In Translation, the rotation, scale and shear parameters are zero, while in a Euclidean transform the scale and shear parameters are zero. So Translation and Euclidean transforms are also stored in a 2 x 3 matrix. Once this matrix is estimated ( as we shall see in the next section ), the images can be brought into alignment using the function warpAffine.

Homography, on the other hand, is stored in a 3 x 3 matrix. Once the Homography is estimated, the images can be brought into alignment using warpPerspective.

Image Registration using Enhanced Correlation Coefficient (ECC) Maximization

The ECC image alignment algorithm introduced in OpenCV 3 is based on a 2008 paper titled Parametric Image Alignment using Enhanced Correlation Coefficient Maximization by Georgios D. Evangelidis and Emmanouil Z. Psarakis. They propose using a new similarity measure called Enhanced Correlation Coefficient (ECC) for estimating the parameters of the motion model. There are two advantages of using their approach.

  1. Unlike the traditional similarity measure of difference in pixel intensities, ECC is invariant to photometric distortions in contrast and brightness.
  2. Although the objective function is nonlinear function of the parameters, the iterative scheme they develop to solve the optimization problem is linear. In other words, they took a problem that looks computationally expensive on the surface and found a simpler way to solve it iteratively.

findTransformECC Example in OpenCV

In OpenCV 3, the motion model for ECC image alignment is estimated using the function findTransformECC . Here are the steps for using findTransformECC

  1. Read the images.
  2. Convert them to grayscale.
  3. Pick a motion model you want to estimate.
  4. Allocate space (warp_matrix) to store the motion model.
  5. Define a termination criteria that tells the algorithm when to stop.
  6. Estimate the warp matrix using findTransformECC.
  7. Apply the warp matrix to one of the images to align it with the other image.

Let’s dive into the code to see how to use it. The comments provide an explanation.

Download Code To easily follow along this tutorial, please download code by clicking on the button below. It's FREE!


C++ code 

// Read the images to be aligned
Mat im1 = imread("images/image1.jpg");
Mat im2 = imread("images/image2.jpg");

// Convert images to gray scale;
Mat im1_gray, im2_gray;
cvtColor(im1, im1_gray, CV_BGR2GRAY);
cvtColor(im2, im2_gray, CV_BGR2GRAY);

// Define the motion model
const int warp_mode = MOTION_EUCLIDEAN;

// Set a 2x3 or 3x3 warp matrix depending on the motion model.
Mat warp_matrix;

// Initialize the matrix to identity
if ( warp_mode == MOTION_HOMOGRAPHY )
warp_matrix = Mat::eye(3, 3, CV_32F);
else
warp_matrix = Mat::eye(2, 3, CV_32F);

// Specify the number of iterations.
int number_of_iterations = 5000;

// Specify the threshold of the increment
// in the correlation coefficient between two iterations
double termination_eps = 1e-10;

// Define termination criteria
TermCriteria criteria (TermCriteria::COUNT+TermCriteria::EPS, number_of_iterations, termination_eps);

// Run the ECC algorithm. The results are stored in warp_matrix.
findTransformECC(
im1_gray,
im2_gray,
warp_matrix,
warp_mode,
criteria
);

// Storage for warped image.
Mat im2_aligned;

if (warp_mode != MOTION_HOMOGRAPHY)
// Use warpAffine for Translation, Euclidean and Affine
warpAffine(im2, im2_aligned, warp_matrix, im1.size(), INTER_LINEAR + WARP_INVERSE_MAP);
else
// Use warpPerspective for Homography
warpPerspective (im2, im2_aligned, warp_matrix, im1.size(),INTER_LINEAR + WARP_INVERSE_MAP);

// Show final result
imshow("Image 1", im1);
imshow("Image 2", im2);
imshow("Image 2 Aligned", im2_aligned);
waitKey(0);

Python code 

# Read the images to be aligned
im1 =  cv2.imread("images/image1.jpg");
im2 =  cv2.imread("images/image2.jpg");

# Convert images to grayscale
im1_gray = cv2.cvtColor(im1,cv2.COLOR_BGR2GRAY)
im2_gray = cv2.cvtColor(im2,cv2.COLOR_BGR2GRAY)

# Find size of image1
sz = im1.shape

# Define the motion model
warp_mode = cv2.MOTION_TRANSLATION

# Define 2x3 or 3x3 matrices and initialize the matrix to identity
if warp_mode == cv2.MOTION_HOMOGRAPHY :
warp_matrix = np.eye(3, 3, dtype=np.float32)
else :
warp_matrix = np.eye(2, 3, dtype=np.float32)

# Specify the number of iterations.
number_of_iterations = 5000;

# Specify the threshold of the increment
# in the correlation coefficient between two iterations
termination_eps = 1e-10;

# Define termination criteria
criteria = (cv2.TERM_CRITERIA_EPS | cv2.TERM_CRITERIA_COUNT, number_of_iterations,  termination_eps)

# Run the ECC algorithm. The results are stored in warp_matrix.
(cc, warp_matrix) = cv2.findTransformECC (im1_gray,im2_gray,warp_matrix, warp_mode, criteria)

if warp_mode == cv2.MOTION_HOMOGRAPHY :
# Use warpPerspective for Homography
im2_aligned = cv2.warpPerspective (im2, warp_matrix, (sz[1],sz[0]), flags=cv2.INTER_LINEAR + cv2.WARP_INVERSE_MAP)
else :
# Use warpAffine for Translation, Euclidean and Affine
im2_aligned = cv2.warpAffine(im2, warp_matrix, (sz[1],sz[0]), flags=cv2.INTER_LINEAR + cv2.WARP_INVERSE_MAP);

# Show final results
cv2.imshow("Image 1", im1)
cv2.imshow("Image 2", im2)
cv2.imshow("Aligned Image 2", im2_aligned)
cv2.waitKey(0)

Reconstructing Prokudin-Gorskii Collection in Color

ECC Image Alignment using OpenCV 3

The above image is also part of the Prokudin-Gorskii collection. On the left is the image with unaligned RGB channels, and on the right is the image after alignment. This photo also shows that by the early 20th century the photographic plates were sensitive enough to beautifully capture a wide color spectrum. The vivid red, blue and green colors are stunning.

The code in the previous section can be used to solve a toy problem. However, if you use it to reconstruct the above image, you will be sorely disappointed. Computer Vision in real world is tough, things often do not really work out of the box.

The problem is that the red, green, and blue channels in an image are not as strongly correlated if in pixel intensities as you might guess. For example, check out the blue gown the Emir is wearing in Figure 3. It looks quite different in the three channels. However, even though the intensities are different, something in the three channels is similar because a human eye can easily tell that it is the same scene.

It turns out that the three channels of the image are more strongly correlated in the gradient domain. This is not surprising because even though the intensities may be different in the three channels, the edge map generated by object and color boundaries are consistent.

An approximation of the image gradient is given below

C++ 

using namespace cv;
using namespace std;

Mat GetGradient(Mat src_gray)
{
Mat grad_x, grad_y;
Mat abs_grad_x, abs_grad_y;

int scale = 1;
int delta = 0;
int ddepth = CV_32FC1; ;

// Calculate the x and y gradients using Sobel operator
Sobel( src_gray, grad_x, ddepth, 1, 0, 3, scale, delta, BORDER_DEFAULT );
convertScaleAbs( grad_x, abs_grad_x );

Sobel( src_gray, grad_y, ddepth, 0, 1, 3, scale, delta, BORDER_DEFAULT );
convertScaleAbs( grad_y, abs_grad_y );

// Combine the two gradients
Mat grad;
addWeighted( abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad );

return grad;

}

Python

import cv2
import numpy as np

def get_gradient(im) :
# Calculate the x and y gradients using Sobel operator
grad_x = cv2.Sobel(im,cv2.CV_32F,1,0,ksize=3)
grad_y = cv2.Sobel(im,cv2.CV_32F,0,1,ksize=3)

# Combine the two gradients
grad = cv2.addWeighted(np.absolute(grad_x), 0.5, np.absolute(grad_y), 0.5, 0)
return grad

Now we are ready to reconstruct a piece of Russian history! Read the inline comments to follow

C++ Code 

using namespace cv;
using namespace std;

// Read 8-bit color image.
// This is an image in which the three channels are
// concatenated vertically.
Mat im =  imread("images/emir.jpg", IMREAD_GRAYSCALE);

// Find the width and height of the color image
Size sz = im.size();
int height = sz.height / 3;
int width = sz.width;

// Extract the three channels from the gray scale image
vector<mat>channels;
channels.push_back(im( Rect(0, 0,         width, height)));
channels.push_back(im( Rect(0, height,    width, height)));
channels.push_back(im( Rect(0, 2*height,  width, height))); </mat>

// Merge the three channels into one color image
Mat im_color;
merge(channels,im_color);

// Set space for aligned image.
vector<mat> aligned_channels;
aligned_channels.push_back(Mat(height, width, CV_8UC1));
aligned_channels.push_back(Mat(height, width, CV_8UC1));</mat>

// The blue and green channels will be aligned to the red channel.
// So copy the red channel
aligned_channels.push_back(channels[2].clone());

// Define motion model
const int warp_mode = MOTION_AFFINE;

// Set space for warp matrix.
Mat warp_matrix;

// Set the warp matrix to identity.
if ( warp_mode == MOTION_HOMOGRAPHY )
warp_matrix = Mat::eye(3, 3, CV_32F);
else
warp_matrix = Mat::eye(2, 3, CV_32F);

// Set the stopping criteria for the algorithm.
int number_of_iterations = 5000;
double termination_eps = 1e-10;

TermCriteria criteria(TermCriteria::COUNT+TermCriteria::EPS,
number_of_iterations, termination_eps);

// Warp the blue and green channels to the red channel
for ( int i = 0; i &lt; 2; i++)
{
double cc = findTransformECC (
GetGradient(channels[2]),
GetGradient(channels[i]),
warp_matrix,
warp_mode,
criteria
);

if (warp_mode == MOTION_HOMOGRAPHY)
// Use Perspective warp when the transformation is a Homography
warpPerspective (channels[i], aligned_channels[i], warp_matrix, aligned_channels[0].size(), INTER_LINEAR + WARP_INVERSE_MAP);
else
// Use Affine warp when the transformation is not a Homography
warpAffine(channels[i], aligned_channels[i], warp_matrix, aligned_channels[0].size(), INTER_LINEAR + WARP_INVERSE_MAP);

}

// Merge the three channels
Mat im_aligned;
merge(aligned_channels, im_aligned);

// Show final output
imshow("Color Image", im_color);
imshow("Aligned Image", im_aligned);
waitKey(0);

Python Code 

import cv2
import numpy as np

if __name__ == '__main__':

# Read 8-bit color image.
# This is an image in which the three channels are
# concatenated vertically.

im =  cv2.imread("images/emir.jpg", cv2.IMREAD_GRAYSCALE);

# Find the width and height of the color image
sz = im.shape
print sz
height = int(sz[0] / 3);
width = sz[1]

# Extract the three channels from the gray scale image
# and merge the three channels into one color image
im_color = np.zeros((height,width,3), dtype=np.uint8 )
for i in xrange(0,3) :
im_color[:,:,i] = im[ i * height:(i+1) * height,:]

# Allocate space for aligned image
im_aligned = np.zeros((height,width,3), dtype=np.uint8 )

# The blue and green channels will be aligned to the red channel.
# So copy the red channel
im_aligned[:,:,2] = im_color[:,:,2]

# Define motion model
warp_mode = cv2.MOTION_HOMOGRAPHY

# Set the warp matrix to identity.
if warp_mode == cv2.MOTION_HOMOGRAPHY :
warp_matrix = np.eye(3, 3, dtype=np.float32)
else :
warp_matrix = np.eye(2, 3, dtype=np.float32)

# Set the stopping criteria for the algorithm.
criteria = (cv2.TERM_CRITERIA_EPS | cv2.TERM_CRITERIA_COUNT, 5000,  1e-10)

# Warp the blue and green channels to the red channel
for i in xrange(0,2) :
(cc, warp_matrix) = cv2.findTransformECC (get_gradient(im_color[:,:,2]), get_gradient(im_color[:,:,i]),warp_matrix, warp_mode, criteria)

if warp_mode == cv2.MOTION_HOMOGRAPHY :
# Use Perspective warp when the transformation is a Homography
im_aligned[:,:,i] = cv2.warpPerspective (im_color[:,:,i], warp_matrix, (width,height), flags=cv2.INTER_LINEAR + cv2.WARP_INVERSE_MAP)
else :
# Use Affine warp when the transformation is not a Homography
im_aligned[:,:,i] = cv2.warpAffine(im_color[:,:,i], warp_matrix, (width, height), flags=cv2.INTER_LINEAR + cv2.WARP_INVERSE_MAP);
print warp_matrix

# Show final output
cv2.imshow("Color Image", im_color)
cv2.imshow("Aligned Image", im_aligned)
cv2.waitKey(0)

Further Improvements

If you were to actually make a commercial image registration product, you would need to do a lot more than what my code does. For example, this code may fail when the mis-alignment is large. In such cases you would need to estimate the warp parameters on a lower resolution version of the image, and initialize the warp matrix for higher resolution versions using the parameters estimated in the low-res version. Furthermore, findTransformECC estimates a single global transform for alignment. This motion model is clearly not adequate when there is local motion in the images ( e.g. the subject moved a bit in the two photos). In such cases, an additional local alignment needs be done using say an optical flow based approach.

You can comment on this post to let me know if you would like a follow up post where I discuss these improvements with supporting code ( obviously! ).




Credits

I got the idea of using the Prokudin-Gorskii collection to demonstrate image alignment from Dr. Alexei Efros’ class at the University of California, Berkeley.

The Ribbon image was obtained from wikiepedia and is in the public domain.

The Prokudin-Gorskii collection is also in the public domain, and images were obtained from the Library of Congress.

Comments

  2. Very nice. I even understood some of the stuff! Wish we had these taught to us in kgp, I learnt nothing much (other than some openGL calls) in my Graphics class !

    Reply

  3. this blog is always super useful. small error in the python code – should be im2 on line 39 of the first example and the comments are switched

    Reply

  5. Thank you sir for nice tutorials. I am using Xcode and working on Image Alignment using your example findTransformECC Example in OpenCV but getting a error: OpenCV Error: Assertion failed (scn == 3 || scn == 4) in cvtColor

    Please suggest.

    Reply

    • Thanks Georgios! For the readers of the blog, I want to mention that Georgios is one of the authors of the ECC alignment paper. So please visit the link to know more information.

      Reply

  7. Thank you for the article. It shows how to use an important tool through a beautiful example. And having both C++ and python codes is also very kind of you.

    Reply

  8. When testing this code to use it on my computer for personal use and fun I get this error: AttributeError: ‘module’ object has no attribute ‘MOTION_HOMOGRAPHY’
    any idea how to fix it?

    Reply

  10. I normally just skip to the relevant code when google sends me to a blog but this is one of the few times I’ve read a post in it’s entirety even after finding the portion I was looking for. Very well written, Dr. Mallick.

    Reply

  11. A very nice article, extremely helpful as I teach myself more about OpenCV. Will you be making the follow-up article with the more advanced techniques for image registration? I would love to see that!

    One question about this article: you use a very high repetitions (5000) and an extremely small accuracy threshold (1e-10)… why doesn’t findTransformECC take forever to finish in your example? In my tests with much smaller iterations and accuracy thresholds but larger input images, it seems to be almost random how long it will take. Even 200 at 1e-6 can sometimes take minutes on 1280×960 source images.

    Reply

  12. Hi. How is this method different from using feature extractions method like SIFT/SURF then use `findHomography` to produce the warp matrix?

    Thank you.

    Reply

    • For many problems, both feature extraction + findHomography and this method will give identical results. This method probably will do better in the presence of large noise.

      Reply

  14. First of all, thank you for such a great explanation with code included. It is really useful.

    I am trying to stitch several images that were taken from a camera moving horizontally, would this work? If not, what would I need to change to make it work?
    Thanks!

    Reply

  15. I want to use this code for a gray scale image. I am unable to perform cv2.findTansformECC when I do so. Do you have any suggestions ?

    Reply

  16. Thank you for your tutorial. It is very nice.

    Could you please tell me more about the local motion in the images? I tried to use image alignment first, and most current motion estimation methods (Brox method, deepflow, SparseToDense, Farneback, DualTVL1, LucaKanade, …) and compensate ROI movement but those are not effective. I want to have stable ROI (in original frames, ROI moved).
    Thank you for your time and consideration.

    Reply

  17. Hello Sir,

    Thank you so much for your helpful blog!
    I am doing image/video stitching. After finding homography i am aligning image with warpPerspective, it gives me output below.
    I am not getting how to solve this ?
    So can you help in this case.

    Regards,
    Kajal
    https://uploads.disquscdn.com/images/9e907a59e2bd565f5a9554d3919104836380dcdf14ed6c86b60d47d4316e92be.png https://uploads.disquscdn.com/images/e1b359a40a4fef9f0e28434f511deaf98a901e3d74353474d34ae285bb7668cb.png

    Reply

      • Hello Sir,

        I mean in question is finding homography between two images and aligning them to stitch but output was weird, so just want to know where is wrong?

        The issue has been solved. I just checked with another test cases (videos) and it works fine. It’s about input giving.

        Thank you so much for you reply!

        Regards,
        Kajal

        Reply

  18. Satya,
    I love your posts, they are very interesting and very useful. I think you do a great job.

    I tried to implement the code from this one, but it seems that I do something wrong for the second one.I cannot figure out what is it, so I need your help.
    I used the Emir image and it keeps giving me an error (please see the screenshot).
    I tried with others images from my PC, but it is the same thing. After doing some more research, I figured out that it seems to be something about the picture size. If I use a small image and termination_eps = 0.6 or bigger, the error does not appear anymore, but the result is not the good one (one third of the initial image appears and the channels are not aligned). I checked the source code for the findTransformECC function and it is almost the same as the one from here, at least in the line from the error and the parts connected. What am I doing wrong?

    I want to use this code (with some adjustments, of course) for all kind of images, without necessarily knowing their sizes. What it would be the appropriate way to do it?

    https://uploads.disquscdn.com/images/79866f5024a1ca96dee943b0bfc4805df6bae26f2a6ac092235b2ce32a3b54b6.jpg

    Reply

  19. Hi Satya:

    What an amazing blog, actually i have to align a big set of images from a multispectral camera and i want to use Cuda with this algorithm, do you know how to do that?, already installed cuda with opencv and i ran some examples succesfully, but i have some problems with this algorithm.

    Thanks for your help

    Reply

  20. Thank you for your work this is so useful. I have tried with images of dimension 1437 x 1243 and it worked fine.

    However, I got a really strange error running it with images of 5472 x 3648 dimensions? 4.37mb photo. I tried running your code with my own images of the above dimensions. I got an error “line 46, in alignment
    (cc, warp_matrix) = cv2.findTransformECC(im1_gray, im2_gray, warp_matrix, warp_mode, criteria)
    cv2.error: D:BuildOpenCVopencv-3.2.0modulescoresrcmatrix.cpp:433: error: (-215) u != 0 in function cv::Mat::create

    ”

    Please you please advice to me what gone wrong with that?

    Reply

  21. Thank you for your work this is so useful. I have tried with images of dimension 1437 x 1243 and it worked fine.

    However, I got a really strange error running it with images of 5472 x 3648 dimensions? 4.37mb photo. I tried running your code with my own images of the above dimensions. I got an error
    “line 46, in alignment
    (cc, warp_matrix) = cv2.findTransformECC(im1_gray, im2_gray, warp_matrix, warp_mode, criteria)
    cv2.error: D:BuildOpenCVopencv-3.2.0modulescoresrcmatrix.cpp:433: error: (-215) u != 0 in function cv::Mat::create ”

    Please could you give me advice on how to do it for big images?

    Reply

  22. Hi Mallick,
    I don’t know if you will still respond to posts on here, but I am trying to realign many images from a webcam that slowly moved position gradually over the day. I’ve used your code, but all I have managed to get out is no image (the aligned image posted is has no dimensions), and the code reaches it’s final position after only 3 iterations.
    My input images are images from a time-lapse camera with slightly different shadow and reflections between the images. See below:
    https://uploads.disquscdn.com/images/74585308d796b411d37830ea25fe8b265298259be39d238b1016d353272e2f60.jpg https://uploads.disquscdn.com/images/82ab23b98dd57f1dae0cf275809a53a1ee9e57f183a60c6b8a34e564a100f477.jpg

    I have many images like this and want to align them together, but it’s just not working. Do you think the change in shadow and reflection is stopping it from working? Is there any way you can get it to work?

    Many many thanks, Eliot

    Reply

  24. Hi Satya, i like your article explanation with the code alot. May I know is there any follow up post with example for the further improvement method that you mentioned?

    Reply

          • This problem struck me some days..And I use my friends’ email do same thing.They cannot receive your email neither. Maybe you should improve your system I think.

          • Thanks. I will report this problem to my email service provider. Can you let me know the region / country so I can include that information when I email my service provider?

          • Actually I have e-maild you about those information.But I don’t sure you have receive my email.And can I download your source code before your service provider involve?

          • Hi. have you receive my email from zyd19****@hotmail.com just now? If you have, please give a response.I am waiting. 🙂

  26. Hello Satya. thanks for the wonderful example. It seems that findTransformECC() function can take several minutes on images larger than a few Megapixels. Since i’m not looking for high level of accuracy, I was hoping to resize my input images down to say 640×480, calculate the warp matrix and then apply that matrix to the higher resolution images however the results seem to be off.. I suspect its due to the fact that the warp matrix needs to be remapped / scaled to the larger size. How do scale the warp matrix so the warpPerspective() will work on the larger resolution images?https://uploads.disquscdn.com/images/1b01fb15aaf53de6886b6cb0126d7ab2ec243db1af64a5fefd9b4abf300c6ab5.png

    Reply

    • I had the same issue yesterday. Understanding the warp_matrix is the key to the solution: the values in the last row denote the translation in pixel units: since you calculate the translation on a lower resolution image (say only 1/5 of the size) you need to scale up the translation factors (in this case by a factor of 5). Leave the other elements of warp_matrix as they are since they denote rotation.

      Cheers, Laurin

      Reply

  27. Hi Satya,

    Great blog. I find myself coming back to it again and again.

    I have a question that I hope you may be able to answer. I’m trying to detect movements in the axis of rotation of an object. If I take a photo, rotate, and take another photo, with the Euclidian option I get the angle of rotation and a transform if any, how do you think I might find the axis of rotation?

    Regards

    Steve.

    Reply

  28. Hello Satya,
    thank you for your tutorials, they are often a good introduction to certain opencv examples for beginners.

    In this tutoria though, it is not needed to calculate gradient images, and in case of more difficult examples than aligning color chanels it may lead to wrong results.

    As described in the original paper and as it can be found in the opencv implementation of findTransformECC, the algorithm itself calculated the image gradients.
    Your example given would make it calculate gradients of the gradient image.

    I tested that with multispectral images (RGB, NIR). In some cases ECC of gradient images fails while ECC of the original grayscale images succeedes. In the other cases both variants fail, or both succeed while using the original images gives a better result.

    Maybe you check this remarks and if you aggree update your tutorial accordingly. It will be even simpler and easier to reproduce. It took me quite some time to searching for other methods to allign my images until I noticed that ECC would work in many cases if I simply not use gradient images.

    Reply

  29. Hi!.
    i’ve similar issue but with id’s like passports, what i want is align the images in other words i want align diferents passports, in this case two, and then extract differences to the passports, like the position some text, symbol, etc. In the example that you give, doesn’t align my images and i imagine that is result from the diferent of data like name, date, photo, etc. I would like if u give me any idea. Thnks

    Reply

    • Hi Elizabeth,

      Unfortunately, I work in ID document analysis ( including passports ) for a client and confidentiality agreement prevents me explaining how it is done. Sorry about that.

      Satya

      Reply

  31. Hi sathya, was just exploring the possibilities with your code,very helpful but as you said it is failing on large misalignment, so I tried in lower resolution image and worked. Can you explain me how to use the warp_matrix calculated on small resolution image on large resolution one? (I tried multiplying last row by the same factor as mentioned in one comment but did not help)

    Reply

  32. Hi Sathya,
    thank you for the post. I was trying to align an image with large misalignment, as you told I calculated the warp matrix on low resolution image. in order to apply this warp matrix on high resolution (original) image what modification I should do. (as mentioned in one comment I tried multiplying last row by same factor but did not help)
    Naveen.

    Reply

Leave a Reply

Your email address will not be published. Required fields are marked *

Learn the state-of-the-art in AI: DALLE2, MidJourney, Stable Diffusion!
Claim Now
This course is available for FREE only till 22nd Nov.
FREE Python Course
We have designed this Python course in collaboration with OpenCV.org for you to build a strong foundation in the essential elements of Python, Jupyter, NumPy and Matplotlib.
  • We hate SPAM and promise to keep your email address safe.
FREE OpenCV Crash Course
We have designed this FREE crash course in collaboration with OpenCV.org to help you take your first steps into the fascinating world of Artificial Intelligence and Computer Vision. The course will be delivered straight into your mailbox.
  • We hate SPAM and promise to keep your email address safe.
 

Get Started with OpenCV

  • FREE OpenCV Crash Course
  • Getting Started Guides
  • Installation Packages
  • C++ And Python Examples
  • Newsletter Insights
  • We hate SPAM and promise to keep your email address safe.

Subscribe to receive the download link, receive updates, and be notified of bug fixes

seperator

Which email should I send you the download link?

  • We hate SPAM and promise to keep your email address safe.
Subscribe To Receive
  • FREE OpenCV Crash Course
  • Getting Started Guides
  • Installation Packages
  • C++ And Python Examples
  • Newsletter Insights
We hate SPAM and promise to keep your email address safe.​
  • We hate SPAM and promise to keep your email address safe.
Subscribe Now
Disclaimer

All views expressed on this site are my own and do not represent the opinions of OpenCV.org or any entity whatsoever with which I have been, am now, or will be affiliated.

Getting Started
Course
Information
About LearnOpenCV

In 2007, right after finishing my Ph.D., I co-founded TAAZ Inc. with my advisor Dr. David Kriegman and Kevin Barnes. The scalability, and robustness of our computer vision and machine learning algorithms have been put to rigorous test by more than 100M users who have tried our products.

Read More
Copyright © 2023 – BIG VISION LLC